DDPM
Paper | Colab code | 中文 Note | 英文 Note |
Hung-yi Lee大神 原理推導影片

概念

Diffusion model 主要在學習如何將 noise 從資料中移除

• 在 Forward step 中，會先給定一個 X_0，在過程中不斷加入 noise，直到變成一個純 noise 的圖像
• 在 Reverse step 會用一個 model 去消除 noise，就可以還原成原始的圖像，為什麼用一個 model 去消除noise，因為在只擁有 noise 的圖像 X_T 的情況下，我們並不知道有哪些 noise 被加在這個影像當中，所以只能靠 model 去預測 noise 的值

但要添加怎樣的 noise ? 還有要添加多少比例的 noise ?

DDPM

Training: Forward step

Forward step(前向過程/擴散過程): 一步步加完噪音(就是個label)之後得到純noise的圖，如果將噪聲變成一個label是不是有可能就可以把圖片還原了

• 在圖片當中加入noise，每一次加一點進去，noise為高斯分布，其實就是不斷輸入image中，最後就變成了個純noise的圖片
• 其實這個過程可以看出不斷建構標籤的過程，有點像是對圖片去做去noise的然後去生成

在論文中，有一個 hyperparemeter β_t 需要自己設定，他影響到添加noise的比例

α_t = 1 - β_t

def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start, beta_end, timesteps)
# define beta schedule
betas = linear_beta_schedule(timesteps=timesteps)

每一個時間點加上的 noise 比例都是不一樣的 (default: 0.0001 ~ 0.02)，所以才有 β，一開始添加一點點 noise 可能原圖就很大，所以一開始 β 會比較低一點。

z_t: 是在 t 時間點的 noise (noise 服從常態分佈)
x_0: 原圖
x_t: 添加t個noise的圖

因為這部分我只選我看得懂的推導，比較艱深/正確的推論方法就請看李大神的影片。

為什麼要設定這個?
其實是因為他們已經先推導過，發現必須要這樣設定才能利用 normal distribution 的公式去再進行推算，否則無法做結合。

所以有了這個closed function之後，只需要原圖x_0和目前是第幾步(t)是多少，就可以求出最後的答案

# forward diffusion
def q_sample(x_start, t, noise=None):
    if noise is None:
        noise = torch.randn_like(x_start)

    sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x_start.shape
    )

    return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise

Sampling: Reverse step 去噪過程

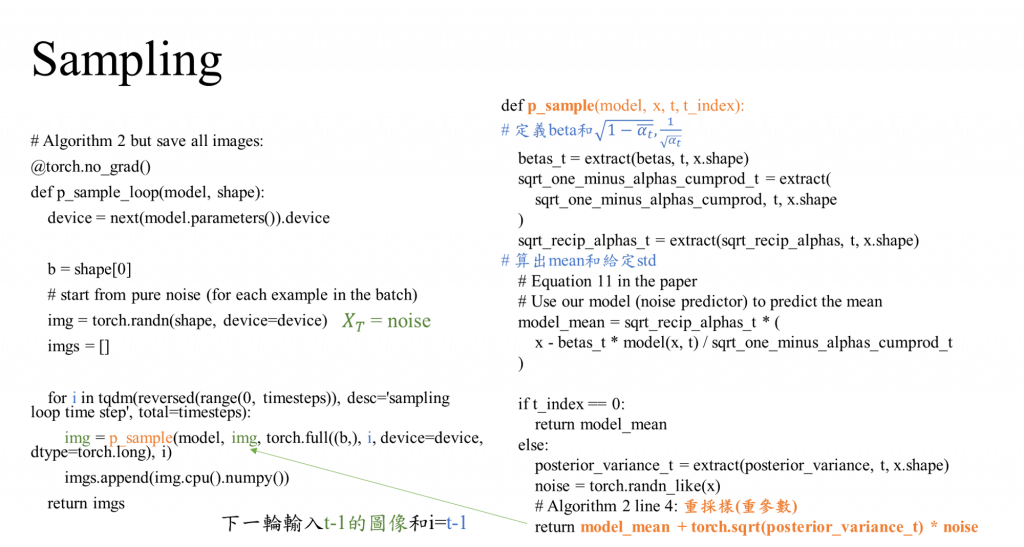
Sampling 逐步還原不帶noise的原圖

因為推導過程比Forward複雜，如果想了解的人李大神會講解。

假設T=200，加完Noise的圖x_T是已知，反推回原圖x_0，直接推回去原圖有點困難，目前還沒做到，而且產生的效果不好，所以他們決定推一推前一個 T = 199 是什麼圖?
最終想要求的東西是P(x_0|x_T)，但這個太難，所以改求P(x_{T-1}|x_T)
可是又不知道x_(T-1)怎麼求，只知道P(x_T|x_(T-1))，所以這邊可以用貝葉式公式

求個近似解，訓練一個模型在x_t時刻的noise z_t是多少?

model 還原的過程中可能會不同，因為預測不出真正的z_t，所以只能靠模型去預測

• 因為z_t看來無法直接求解，只能訓練一個模型來計算
• 這些相關論文都用 UNet，是常用在 segmentation 任務上
• 模型輸入有兩個參數，一個是當前時刻的分布x_t和時刻t

posterior_variance 是為了增加推理中的隨機性，而額外增添的一項。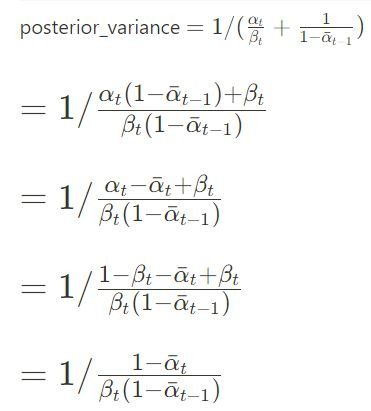

在DDPM論文中，已透過實驗證明β_t = σ^2可用，所以為了計算方便，源碼中也選用了後者β_t = σ^2。

model_mean = sqrt_recip_alphas_t * (
        x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
    )

Training Model 詳細架構

實際做法

要對一個time做成位子embedding, Tensor(128, 112)
對這個time embedding做成 Tensor(128, 28)，要跟x做一個結合
在transformer當中 x+position embedding得到實際x的code
輸出如下 tensor(128,28,28,28)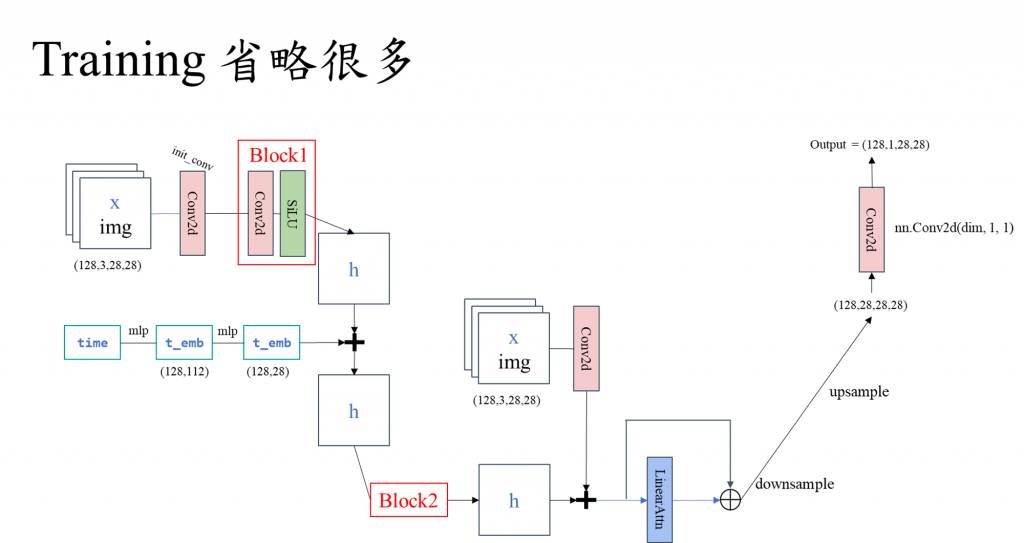

本篇是DDPM 是將時間資訊直接做加法
後續改進新版的CILP是融入圖的feature和文本的feature和時間
CILP的ATTN是可能有意義的，他可能圖像的某個特徵是跟文本上有對應